De mens in de kijker (2).
Een optisch onderzoek naar de aura van de hand.
In zowat alle tijden en in bijna alle niet-westerse culturen verneemt men getuigenissen van mensen die beweren dat wij niet alleen een biologisch lichaam hebben, maar dat wij eveneens beschikken over een geheel van fijnstoffelijke lichamen, die samen de zogenaamde aura uitmaken. Deze zou zich in enkele ijler wordende lagen rondom het biologische lichaam bevinden. Volgens zowat alle niet westerse culturen zouden bovendien sommige plaatsen met die mysterieuze fijne stof meer geladen zijn dan andere. Men spreekt van een ‘Hylisch pluralisme’. ‘Hylè’ is het Oudgriekse woord voor ‘stof’, ‘materie’, en pluralisme slaat op een veelheid van soorten. Heden wordt het mogelijk bestaan van zulk een fijne stof, die overigens niets met kernfysica te maken heeft, in heel wat middens sterk betwijfeld. En als je er vrij zeker van bent dat iets niet bestaat, dan ga je er uiteraard ook niet naar zoeken. Anders ligt het evenwel als je een stil vermoeden hebt dat over dit onderwerp het laatste woord nog helemaal niet is gezegd. Dan is er iets in je dat je bij herhaling aanspoort om toch nog wat verder te blijven zoeken…
In 1687 had Isaac Newton met zijn boek ‘Principia Mathematica’ de basis van de klassieke mechanica vastgelegd. Hierbij ging hij uit van een vast coördinatenstelsel dat iedere plaats- en tijdbepaling ondubbelzinnig vastlegde, en van een standaardtijd, een tijd, die om het even waar in het heelal, steeds even snel zou verlopen. Met de sterke ontwikkeling van de wetenschap op het einde van de 19de eeuw leek het vinden van een vast oriëntatiepunt in een steeds verder uitdijende sterrenruimte, een onmogelijkheid. Dus hoopten sommigen dat de ruimte tussen de sterren misschien gevuld zou zijn met een soort van gelijkmatig verdeelde, uiterst fijne en onzichtbare ‘sterrenstof’ die als zulk een vaste referentie zou kunnen dienen. En deze stof zou ook de lichtgolven dragen, net zoals lucht de geluidsgolven draagt.
De gedachte aan zulk een fijne stof, of ‘ether’, zoals men dat toen heette, kwam weer in de aandacht van de wetenschap. Mocht zulk een ether bestaan, dan zou de aarde in haar cirkelvormige baan om de zon soms met die ether mee bewegen, en soms tegen die ether in. Dit zou dan leiden tot een verschil in lichtsnelheid, zo dacht men. Licht dat met de ether mee beweegt, zou dan een hogere snelheid hebben dan licht dat hier tegen in gaat. En dat wilden Michelson en Morley in 1887 nagaan. Ze vonden evenwel geen verschil in snelheid en ook geen sterrenstof. Sedertdien is het geloof aan het bestaan van de ‘uniforme ether’ als voortplantingsmedium voor het licht verlaten. En bij veralgemening geraakte ook het bestaan van elke andere soort van fijne stof in de vergetelheid. Een beschrijving van dit beroemde experiment dat wij, in wat hierover nog volgt, verkorten tot het M&M-experiment vind je op de knop hieronder.
Starten we ons onderzoek met het effectief bouwen van de opstelling, vereist voor het uitvoeren van de foucault-test. De test werd in 1858 door de Franse natuurkundige Léon Foucault beschreven. Fouten die ontstaan bij het ‘slijpen’ van sferische spiegels kunnen hiermee zichtbaar gemaakt worden en dit tot op een onderdeel van een golflengte van het licht. Het is zowat een standaardtest, en is gekend bij bijna alle amateur-spiegelslijpers. Door het weloverwogen over elkaar schuren van twee glasschijven, waartussen zich een brei van harde korrels bevindt, wordt de bovenste glasschijf geleidelijk hol, en de onderste bol. Eens afgewerkt zal de eerste van een spiegelende laag voorzien worden en zal uiteindelijk als spiegel voor onze kijker dienen. Zulk een spiegel vangt heel wat meer licht op dan ons oog. De grote lichtsterkte van een kijker leidt tot het waarnemen van sterren die voor ons anders onzichtbaar zijn. We vragen ons af of er dan ook andere, nog verborgen dingen zijn, die we met de kijker kunnen zichtbaar maken, zoals b.v. een luchtturbulentie rond onze hand. Of misschien moeten we onze ogen wat beter aan het duister laten wennen, en pas daarna kijken.
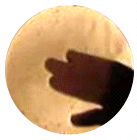

Dan wordt het een verhaal van ‘kegeltjes’ en ‘staafjes’. In daglicht zijn de kegeltjes in ons oog heel wat actiever. Ze zorgen ervoor dat we de kleuren goed van elkaar kunnen onderscheiden. In de duisternis zijn onze staafjes meer van dienst. Dan tonen ze ons een schemerig spel van licht en schaduw. En misschien brengt die duisternis ook in onze foucault-opstelling toch iets meer aan het licht dan we op het eerste gezicht zouden vermoeden. Daarom voorzien we onze lichtbron van een dimmer. En we kijken in onze opstelling niet alleen als ze behoorlijk verlicht is, maar ook als ze meer in het duister is gehuld. Doen we dat, dan zien we eerst onze hand behoorlijk verlicht, en daarna, in een bijna totale duisternis, merken we een flauwe, nevelige en lichtende band rondom onze hand.
Bij het uitvoeren van het Michelson en Morley-experiment werd voor het eerst in de geschiedenis gebruik gemaakt van interferentie van licht. Het kleurenspel in een zeepbel of in een olielaagje op een plas water zijn b.v. het resultaat van optische interferentie, van het samenspel van vele lichtstralen.



Of nog: houden we het scherm van onze GSM (die af staat) zo dat we er het zonlicht of het licht van een lamp in weerspiegeld zien, dan merken we hierop eveneens een aantal prachtig gekleurde lijnen.
Zeepbellen, olievlekken en GSM-schermen hebben door hun uiterst dun en doorzichtig laagje iets van een ‘interferometer’. In principe gaat het om een lichtbundel die aan de boven- of onderzijde van zo een laagje wordt weerkaatst, en zo in twee deelbundels wordt gesplitst. Elk deel legt een iets verschillende weg af, of ondergaat een verschillende verstoring, waarbij nadien de bundels weer met elkaar worden verenigd. Zijn de onderscheiden bundels bij hun doorgang in de opstelling helemaal niet vervormd, dan ontstaat bij hun vereniging een welbepaald interferentiepatroon, b.v. een aantal verticale strepen zoals weergegeven op de tekening hierboven rechts. Is de ene deelbundel echter verschillend van de andere, of verschillen ze beiden t.o.v. elkaar, dan kan dit zijn weerslag hebben op interferentiepatroon. De strepen kunnen b.v. vervormd zijn. De aard van de vervorming geeft dan informatie over de kwaliteit of kwantiteit van het doorzichtige laagje dat doorlopen werd.
Trachten we vervolgens ook effectief een soort van interferometer te bouwen. Gaan we na of er zich een interferentiebeeld toont. En vervolgens kijken we of we dit beeld kunnen verstoren met onze hand in de lichtweg te brengen.


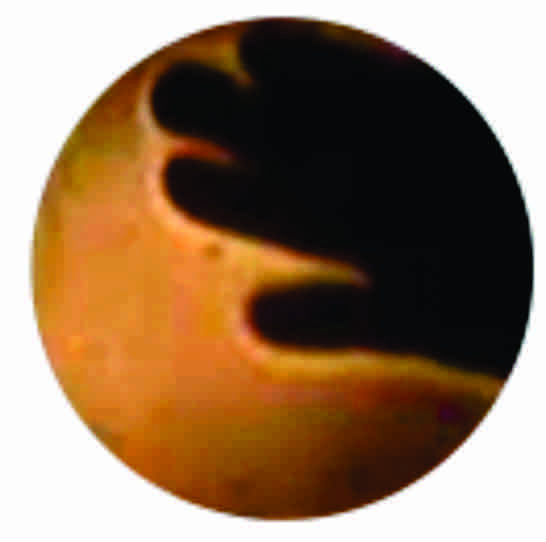
Het lukt ons om mooie interferentielijnen in beeld te krijgen. Sterker nog, bij het bijzonder nauwkeurig afstellen wordt één lijn zelfs heel wat breder dan het spiegeloppervlak. We zien mooie en hevige interferentiekleuren. Brengen we de hand in de lichtweg dan ontstaan gekleurde slierten van opstijgende lucht. Onze hand is warmer dan de lucht rondom, waardoor deze turbulenties ontstaan. Deze hebben een andere brekingsindex zodat daar de interferentie-kleuren zich wijzigen. Verduisteren we vervolgens de opstelling maximaal, dan zien we geen slierten meer, maar toont zich opnieuw de flauwe, nevelige en lichtende strook rondom de hand, zoals we die ook al vaststelden bij de donker-opstelling van de foucaulttest.
Werpen we twee stenen tegelijk en op een korte afstand van elkaar in het water, dan zien we de golven, veroorzaakt door de ene steen, de golven van de andere steen ‘doordringen’. Waar twee toppen elkaar raken, is het waterpeil hoger, waar twee dalen elkaar raken, is het peil lager. Waar een top een dal vult, blijft het water even hoog. Dat werd in het vierde hoofdstukje al toegelicht.
Licht beweegt zich ook in golven. Raken onder welbepaalde omstandigheden twee golftoppen elkaar, dan is het licht dubbel zo intens. Dat is ook zo wanneer twee dalen in elkaar overvloeien. Wanneer echter een top een dal vult, heeft men het merkwaardige verschijnsel dat licht toegevoegd aan licht… duisternis geeft.
Hetzelfde principe, maar nu toegepast op geluid, kennen we bij een ruis-onderdrukkende hoofdtelefoon. Van een ontvangen geluidsgolf wordt een kopie gemaakt die dan met een vertraging van een halve golflengte aan het oorspronkelijke geluid wordt toegevoegd. Hier leidt de som van deze twee geluiden dan tot… stilte.
Zou het ons ook lukken om een interferometer te bouwen, waarbij de beide deelbundels zich met een verschil van een halve golflengte (of een veelvoud van een aantal oneven golflengten) zouden verenigen? Bekomen we dan ook duisternis? Wat zal er zich tonen als we dan de hand in de lichtweg brengen? Na heel wat denkwerk en vele praktische moeilijkheden lukt het ons. Kijken we, dan zien we een brede band, of zelfs het hele spiegeloppervlak, gehuld in destructieve interferentie. Brengen we onze vinger in de lichtweg, dat wordt dit zo subtiele evenwicht verstoord en zien we opnieuw een lichtende band rondom de vinger. Ditmaal toont er zich geen flauwe nevel zoals we dat wel zagen bij de Foucault-test. Wel zien we de gele interferentiekleur, grenzend aan de zwarte destructieve interferentie.


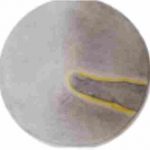
Een reversal-interferometer geeft een beeld, tezamen met het spiegelbeeld. Brengen we b.v. de vinger in de eerste helft van de lichtweg, b.v. in de linkerhelft, dan zien we in de rechterhelft van de spiegel diezelfde vinger verschijnen, maar nu links-rechts omgekeerd. Zowel in een lichtsterk veld, als in een lichtzwak veld leidt dit tot merkwaardige beelden.
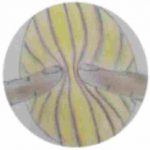
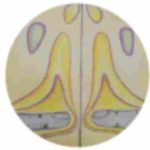

De eerste twee tekeningen tonen wat er te zien is bij volle lichtsterkte. Bij het laatste beeld is het licht gedimd en zien we weer een flauw-lichtende band rond de vinger en diens spiegelbeeld. In wezen brengen we op die manier een verstoord beeld samen met een niet verstoord beeld.
Tot hiertoe hebben we onze interferentie-opstellingen beperkt tot twee deelbundels die zich met elkaar verenigen. Maar zou het lukken om b.v. twee interferenties met elkaar te laten interfereren? Wat zal er zich dan tonen? En zou dit mogelijkheden kunnen geven om opstellingen te bouwen die nog heel wat gevoeliger zijn dan een enkele interferentie van ‘slechts’ twee deelbundels?



We kijken tenslotte terug naar het M&M-experiment dat we bij de aanvang van deze tekst hebben vermeld. Het toonde inderdaad geen uniform verdeelde fijne sterrenstof aan. Sommigen veralgemeenden dat hiermee het hele gegeven ‘fijne stof’ dan ook niet strookte met de werkelijkheid. Na alle voorgaande experimenten kan men zich toch afvragen of die harde conclusie toch aan enig voorbehoud onderhevig is.
Doordenken we het experiment van Michelson en Morley. Bij ons weten werd het uitgevoerd met een lichtbundel die in twee deelbundels werd gesplist, die elk op een vlakke spiegel weerkaatsten en nadien weer verenigd werden en met elkaar interfereerden. Er is dus helemaal geen holle spiegel en geen divergerend of convergerend licht bij betrokken. Geen der beide deelbundels binnen in de opstelling werd verstoord. Dat was ook niet de bedoeling van het experiment. De aandacht was gericht op wat er zich eventueel buiten de interferometer zou bevinden : de uniform veronderstelde fijne sterrenstof.
En wat zo we het M&M-experiment overdoen, maar nu in een enigszins gewijzigde versie. Dan komt het ons voor dat er met dit experiment inderdaad geen – weliswaar uniform verdeelde – fijne stof buiten de opstelling te vinden is, maar dat binnen in de opstelling juist wel het bestaan ervan kan aan aangetoond worden. En als dat zo zou zijn, dan lijkt ons dat toch een merkwaardige speling van het lot. Een opstelling, bedoeld om het bestaan van (uniforme) fijne stof te ontkennen, lijkt dan, in een gewijzigde vorm, het bestaan van fijne stof juist wel te bevestigen.



Met onze grootste telescopen hebben wetenschappers de ruimte tot in zijn verste uithoeken verkend. Wat reikt het blikveld van de hedendaagse mens toch ontzettend ver. En de weg naar onszelf? Reikt die ook zo ver? Wat zo die machtige wetenschap de mens, onszelf ook eens – letterlijk – in de kijker zou zetten? En dit met materialen en met een precisie waar een amateur-knutselaar slechts kan van dromen. Welk een schat aan nieuwe informatie over onszelf zou ons dit kunnen opleveren? Het blijven vooralsnog erg boeiende en intrigerende vragen. We lichten dit alles toe in een afzonderlijke tekst.
Een aantal wetenschappers lijkt – zacht gezegd – niet erg ingenomen te zijn met dergelijke experimenten. Alles wat enigszins naar het paranormale neigt, zou volgens hen niet echt een onderwerp van wetenschappelijk onderzoek kunnen zijn. Wie thuis is in de geschiedenis van de wetenschap zal dit nauwelijks verbazen. We hadden het op deze site al eerder over het onderscheid tussen een methodische en een ideologische vorm van wetenschap.

